Wrist-spin and the Magnus effect

Having looked at various websites and publications with sloppy descriptions of the aerodynamic forces involved in wrist-spin bowling, the one-time A-grade A-level physicist and wannabe aerodynamicist in me has forced me to have a go at describing these effects myself.

So, the Magnus effect. Lets be clear - this isn't the effect that swing bowlers use. In cricket it is a force mainly utilised by spinners, particularly wrist-spinners as they get the ball spinning fastest.

The history of the Magnus effect

The Magnus effect was first discovered when man invented the cannonball. When round projectiles were fired from a firearm, the ball would grip one side of the barrel, making it spin, and instead of flying straight would curve off right, left, up, down or any which way. This was rather frustrating (unless you were the person being fired at!) and there are some estimates that old unrifled firearms managed to hit their intended target less than 5% of the time.

Heinrich Magnus is the person the effect is named after, having described it in 1852 while investigating how to make German artillery more accurate. It had previously been correctly diagnosed by Isaac Newton in 1674 while watching a game of tennis, as well as being observed by British artillery scientist Benjamin Robins in 1742, which led him to suggest rifling. Somehow, though, the Magnus got the credit...

The Basics

Before you brace yourself for the science, let's get just one vital term straight. Imagine that the Earth is a cricket ball, and that the seam is the Equator. Then imagine a line straight through the ball going in at the north pole and out at the south pole. When the ball is spun around its seam by a spinner, this line through the ball is the axis around which the ball rotates, and has a rather unoriginal name: the Axis of Rotation.

I'll mainly deal with the axis of rotation in terms of what it means for the aerodynamic forces on the ball, but there's one important thing I ought to make clear: When a body is spinning it is subject to gyroscopic effects that require a large force to change it's rotational axis. The practical upshot of this is that the axis of rotation of a spinning ball as it leaves the hand will remain virtually unchanged until the ball pitches. I have sometimes observed that on TV a spinner's delivery appears to change its axis of rotation in flight, and after much head-scratching I'm pretty sure this is an optical illusion caused by the strobe effect of the camera, as I've never observed this effect with my own eyes.

Getting back to Magnus, imagine a golf ball contentedly sat on its tee. Golfers have learnt over the years that they need to slice underneath the poor defenceless little ball as they tee off, so that the ball travels towards the hole with the underside moving towards the hole and the top side moving away. They do this because when a ball travels trough the air and spins around an axis of rotation that is a) horizontal, and b) perpendicular to its direction of motion, the air around the ball will push it upwards. This means the ball will take off as it leaves the tee, allowing the golfer to hit the ball further.

I use the example of golf because almost uniquely among sportsmen a golfer only ever intends to use the force of the Magnus effect in one direction - upwards. If at any point you get a bit lost and find yourself confused as to which way to spin a ball to get it to move in the intended direction, just remember: Golfers only ever intend to lift the ball up, and they only ever use backspin.

How it Works

So to explain exactly how the effect comes about, lets take a look at a spinning golf ball in a wind tunnel:

(I took the top image from this website - the annotations in the picture under that are my own)

Actually what you see here is a spinning golf ball in a water tunnel, with a dye squirted onto the front face of the ball to show the flow of the water around it. The water isn't moving very fast, but because water is much more viscous and less compressible it is analogous to what happens in air.

Looking at the two arrows indicating the spin of the ball, the top edge of the ball is travelling backwards, and the bottom edge is moving forwards. The effect of this is that the top edge behaves like a ball that is moving through the air slower than the spinning ball actually is, while the bottom edge acts as if it is travelling faster. When a ball travels through the air at speed, it creates a wake. If it travels through the air slower the air is more able to get around the ball, making the wake smaller. And if it travels quicker the wake gets bigger, until at some point the flow becomes turbulent.

So therefore, and as the picture shows, the side of the ball travelling slowly through the fluid creates a small, smooth wake while the faster side creates a larger, turbulent wake. This lopsided wake means the air is propelled downwards, and because momentum is conserved this results in an upwards force on the ball. This force is what creates the Magnus effect.

Wrist-spin Applications #1: The Top-spinner

I've started with the top-spinner rather than the stock legbreak as this is by far the easier delivery to describe, so it's a good starting point. I'm assuming it's a "pure" top-spinner, i.e. that the seam is vertically upright and pointing down the wicket.

Essentially, all you have to do to work out what the Magnus effect will do with this ball is take the golf ball and turn it upside down, so that instead of pushing the ball up it pulls it down instead.

Now here, for once, I have to take issue with Peter Philpott. In his otherwise flawless book "The Art of Wrist-Spin Bowling" he describes the effect of top-spin (he calls it overspin) saying that "overspin increases the effect of gravity", a bit of sloppy science that will have all the physics teachers rolling their eyes. The effect of gravity is unchanged throughout - what top-spin does is add an additional effect which accelerates the ball in the same direction. So the ball has the downward acceleration due to gravity AND some more downward acceleration due to the Magnus effect on top of that.

So as the batsman sees the ball come out of the bowler's hand, he will judge the speed and angle and intuitively estimate where the ball will pitch based on downward acceleration due to gravity alone. Thereafter the Magnus effect will make the ball dip faster in the air, and bounce further away from the batsman than he originally thought it would. That's not all, however. Because the ball has dipped it will now hit the ground at a steeper angle, and therefore it will bounce higher.

Now anyone who has ever spun a ball onto the floor in front of them will find this last part counter-intuitive. If you gently chuck a top-spinning ball onto the floor in front of you the traction as it lands will accelerate it away from you, making the angle it bounces up at shallower. Likewise a back-spun ball will seem to sit up, and if you give it a really good rip you can even get it to bounce right back towards you despite its original momentum. However - and spinners need to get their heads round this - at any significant speed the Magnus effect's ability to make the ball hit the ground at a steeper angle and thus bounce harder and higher far outweighs this effect. It's not that the effect doesn't exist, after all it's the same force that makes a leg-break turn, it's just that it is dwarfed by a counter-acting force in this situation.

So the Magnus effect will make a top-spun ball dip more during flight, meaning it will pitch shorter than anticipated, and hit the ground at a steeper angle, making it bounce higher.

Wrist-spin Applications #2: The Back-spun Flipper

The back-spun flipper (and again I'm assuming a vertical seam, facing down the wicket, only spinning the other way now) is similar in it's aerodynamic effect to the top-spinner, but obviously it's the other way round. Now the acceleration due to the Magnus effect is in the opposite direction to gravitational acceleration, so the spin cancels out part of the downward acceleration, flattening the trajectory of the ball. As with the golf ball the slider will pitch further away from where it was delivered than an unspun ball would. This means it keeps high and pitches closer to the batsman than his initial assessment would suggest. As with the top-spinner, the Magnus effect changes the way a flipper bounces off the pitch, this time reducing the bounce as the ball will hit the ground at a shallower angle.

Wrist-spin Applications #3: The "Square" Leg-Break

Now here's a tricky one. The seam is vertical and the axis of rotation points straight down the same line as the direction of travel, and as such you'd expect there to be no effect on the ball whatsoever. Indeed, many textbooks will tell you there's no effect - I've seen at least two that say this - but it just ain't so!

To understand how a square leg-break uses the Magnus effect to generate drift, I'm afraid I'm going to have to teach you a little applied mathematics. Firstly there's the difficult subject of vectors. Think of it like this: as the ball goes from bowler to pitch it is moving in two different directions at the same time, with two different forces acting on it. Firstly it is travelling horizontally down the wicket, and is held back by wind resistance, and secondly it is travelling vertically, first up into the air and then down onto the pitch as gravity attracts it towards the Earth. Or to put it another way, as you bowl the ball up to get some flight, it leaves your hand at a particular speed diagonally upwards that can be split into two component velocities: towards the batsman so that it reaches him after a certain time, and up into the air so that as it accelerates downwards it travels a certain distance horizontally before pitching, which dictates your length.

Well it turns out that spin - or, to call it by it's proper scientific name, angular velocity - can also be split into component angular velocities around axies other than the actual axis of rotation. Think of a spinning ball in your mind, first with the axis of spin the same as the direction of travel. At this point the drift is zero. Now imagine turning the ball slightly, and there will be a small amount of drift, increasing gradually until the axis is perpendicular to the direction of travel - this is the point of maximum drift. Between these two points the drift will be some fraction of the maximum.

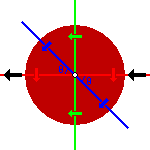The diagram on the left represents the view from the side of a ball bowled by a right-arm wrist-spinner. The black arrows show the direction of travel, the blue line shows an axis at an angle to the direction of travel, the red axis is the axis of zero Magnus effect where the angle is 0, the green line shows the axis of maximum effect where the angle is 90 degrees, and the coloured arrows show the motion of the closer side of the ball as it spins. As the angle increases from zero, the percentage of the maximum drift generated varies as follows:

0 degrees: 0 % drift

15 degrees: 25.9 % drift

30 degrees: 50.0 % drift

45 degrees: 70.7 % drift

60 degrees: 86.6 % drift

75 degrees: 96.6 % drift

90 degrees: 100 % drift

This means the ball can be subject to a portion of the Magnus effect at any point where the axis of rotation is not directly along the line of travel. The reason most textbooks overlook this effect is that they lazily forget that the ball is not travelling in a straight line: it travels in a curved path up and down due to gravity, and hence the Magnus Effect does come into play, since the ball's axis of rotation changes relative to its direction of motion, despite remaining horizontal at all times relative to the ground.

How the Magnus effect varies over the ball's trajectory

To demonstrate this I've imagined a stock leg-break that is released 2 metres above the ground, takes 1 second between leaving the bowler's hand and hitting the pitch (for simplicity, and it means he's bowling at a realistic 47.9 mph), and pitches four yards from the wicket (a reasonably standard length for a wrist-spinner):

One thing that's important to note: Magnus effect is proportional to speed, and gravity and drag will change the ball's speed over the course of its trajectory. I calculated the ball's trajectory on a spreadsheet, including a slightly rough-and-ready but reasonably representative simulation of wind resistance. The ball leaves the hand at 47.9 mph, slows to 35.6 mph as it pitches and averages 38.1 mph over this distance. From here on when I talk about the proportion of maximum Magnus effect being generated, I'm factoring in the instantaneous speed and working the force out relative to the maximum possible at the average speed.

Marked on the picture are five points in the ball's flight:
A) the point at which the ball leaves the bowler's hand
B) the highest point the ball reaches
C) the point at which the ball falls level with point A
D) the point equidistant between C and E
E) the point immediately prior to the ball pitching

The black arrows in this picture shows the direction of travel of the ball at each point as seen from side-on:

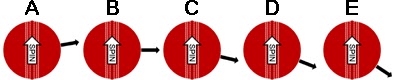
Now let's swivel those round to see how the ball is spinning relative to the direction it's travelling in:

NB: the axis of rotation is not changing, it's the direction of the ball's motion that is different!

At A, the ball has left the bowler's hand travelling diagonally upwards at an angle of just under 10 degrees to the horizontal. The component of Magnus effect is just over 1/5th what it would be if the seam was angled in the same direction the ball was travelling, and it will push the ball towards the off-side. As the ball approaches the peak of its trajectory at B, the Magnus effect wears off until the axis of rotation is the same as the direction of travel and no force is felt. Then as the ball comes back below this point towards C the Magnus effect comes back, this time pushing the ball to leg, so that as the ball reaches C the force on the ball is now working in the opposite direction. By D the ball has slowed down to its minimum speed, gravity accelerating it down from here on, ramping up the drift to leg until at E the ball hits the ground at an angle of 38 degrees generating a shade under 2/5ths of the maximum drift just before it does so.

You will note that for more than half of its journey the ball is travelling downwards to some extent, and this leads me to venture that one rarely mentioned but important aspect of giving the ball flight is not just to get the ball above the batsman's eyeline, but also to maximise the ball's speed and angle of attack over this diagonal section and thus increase the ball's drift in the last few moments before it reaches him.

The "laid-back" leg-break

The example above is a simple one, but a more realistic representation of how leg-spinners actually bowl would be to have the ball coming out of the hand with the axis of rotation already in the same direction as the ball is travelling. This time the seam position at the five points looks like this from side-on:

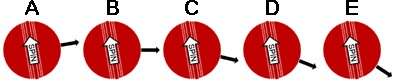
And so we then look at the seam relative to the direction of travel:

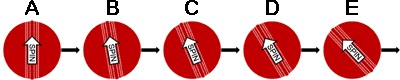
Now you'll see that at A the ball starts with no drift, as the axis of rotation and direction of motion are the same. However, as soon as it leaves the hand its downward acceleration due to gravity starts to create an angle and so produce drift, and this time it's all drift towards leg. By E the ball has an angle of attack of more than 43 degrees, generating nearly 2/3rds of the maximum drift. All this extra drift, and the fact that it only drifts one way, mean that assuming the spin on the ball is the same this ball lands an extra 2/3rds further to the leg side of the pitch than the example above.

Obviously there's a limit to the sideways drift you can get before you've angled the ball so much that the seam won't grip the pitch, but let me remind you - the difference in angle between these two deliveries is less than 10 degrees...

Remember - this ball will start to drift straight out of the hand, and all the more so because it's at its fastest at this point. Now look back at that leg-break with the vertical seam - remember how it drifted to the off-side as it left the bowler's hand, then drifted back the other way further on? Well, doesn't that suggest that a googly bowled with a vertical seam will drift to leg to begin with, initially making it look like a laid-back leg-break? Interesting, VERY interesting...

Magnus À La Carte

Now since you only need components of spin to generate either dip/lift (in the case of the topspinner and slider) or drift (in the case of the leg-break) it follows that if you have components of both you can have your cake and eat it - and so you can!

The overspun leg-break is a good example: the seam is rotated back to generate a little extra sideways drift (like the laid-back leg-break) and also swivelled round part of the way towards a top-spinner to give it some dip. Not only that though - because the top-spin will make the ball dip more sharply towards the end, this more downward angle will act to increase the sideways drift, as will the added speed from a steeper fall!

Now go back to the slider - one really useful aspect of this delivery is that the shallower angle means that a backspun ball  doesn't have to be travelling as fast as an unspun ball to pitch in the same place - hence it follows that if you can bowl accurately enough, a bit of backspin can be used to very effectively disguise a slower ball, and of course that means topspin can equally be used to disguise a faster ball.

There are any number of permutations so I won't list them all here, just rotate that golf ball round every which way, remember how drift varies as the ball rises and falls, and work it out for yourself.

Factors affecting the Magnus force

So far I've only mentioned three factors which change the amount of force generated - the angle of the axis of rotation, the amount of spin on the ball and the speed the ball is travelling. There are many more and I'll attempt to list them here.

Firstly there's wind. This is a fairly obvious one as it changes the effective speed of the ball through the air. Then there's air density. The effect is generated as you'll remember by pushing air to one side, so if the air being pushed aside is heavier, the Magnus force will increase. There are many factors that will make up the density of air, such as altitude, air temperature (cold air is denser), humidity (humid air is actually less dense than dry air) and of course there's the ambient air pressure which is down to the weather. Clearly, there's nothing a bowler can do to change any of these factors, except to persuade the captain to let him bowl into the wind.

Then there's the dimensions of the ball. Firstly increasing the size of the ball will generate more force, and then the mass of the ball will reduce the amount of movement. Note that the mass doesn't affect the amount of force generated, but it will reduce the acceleration that that force produces, so less drift. There's a bit of leeway in the Laws about how large and heavy a ball can be when new, and also a ball can change size and weight as a match progresses, but I'd imagine these two factors will often tend to cancel themselves out.

The size of the seam may also have an effect, at least when the seam's spinning at an angle to the ball's motion, as this will disrupt the airflow over the ball. I seem to recall reading somewhere that leg-spin's relative decline from the 1960s onwards may have had something to do with growing seams meaning less traction off the pitch, but I'd venture to speculate (and it is pure speculation) that this growing of the seams also affected the aerodynamic properties of the ball.

Finally, and this is an important factor, there's the quality of the surface of the ball. Without going into too much detail, a rough ball will allow the air to grip to it better at slow speeds, while at higher speeds the reverse happens and the rough surface will make the airflow more turbulent. This is how swing bowlers get their swing, and explains how conventional swing can be reversed above a certain speed and with the rough side facing the other way. Anyway, all a wrist-spinner really needs to know is that a rougher ball will make the difference in flow over the two sides more extreme and thus will be able to get more Magnus effect. So if you've ever wondered why you get more drift practising with old beat-up balls than you can in the opening overs of a match, this would be why!

Disclaimer...
Some of this stuff is fact, and some of it is based on my own logical interpretation of things I've seen, read or thought about. It's very probably a pretty good explanation of how the Magnus effect works, but don't go basing a thesis on it!